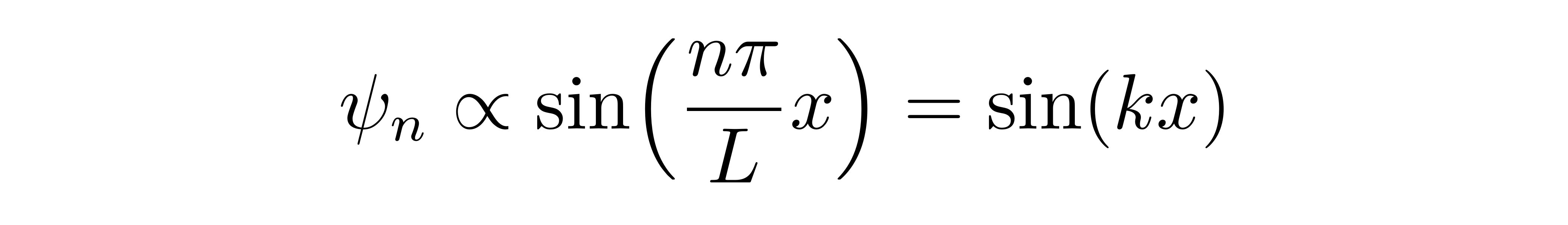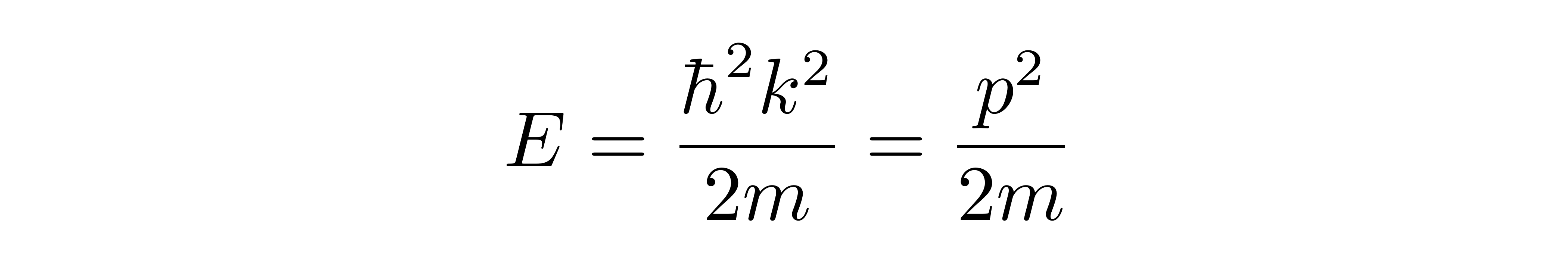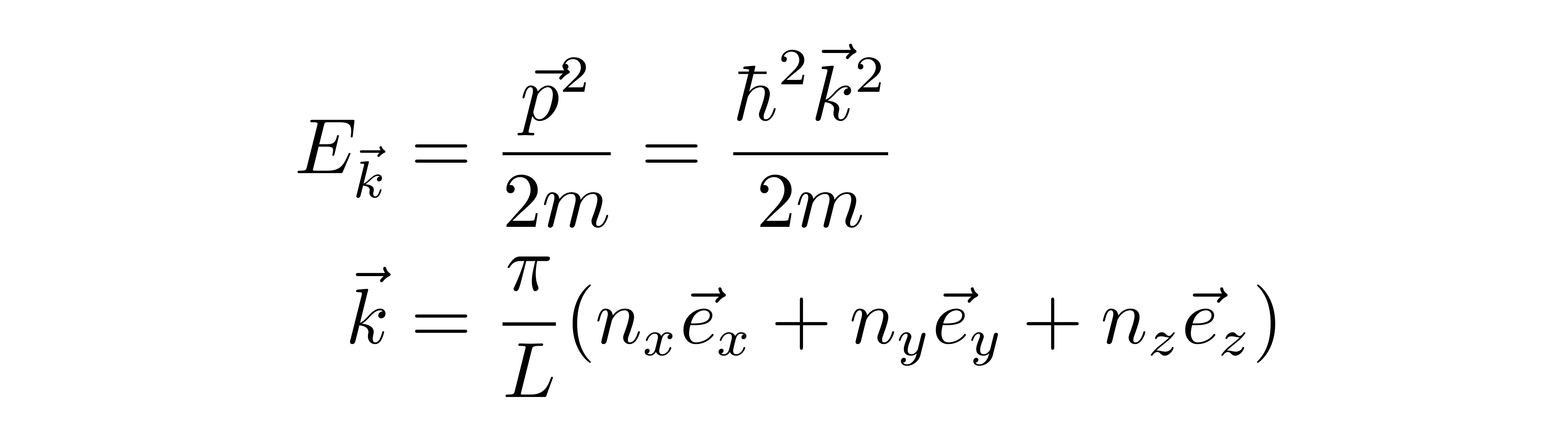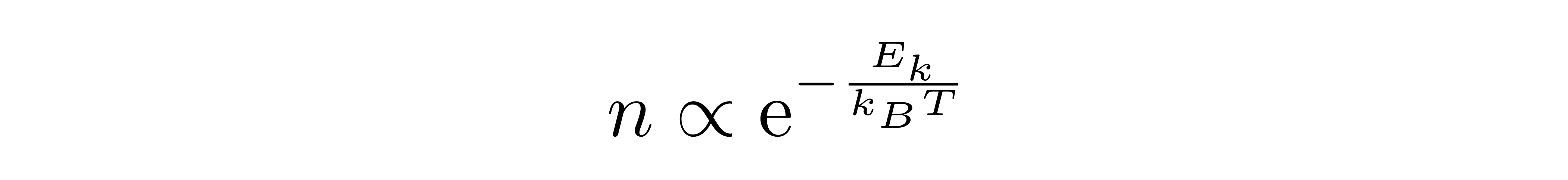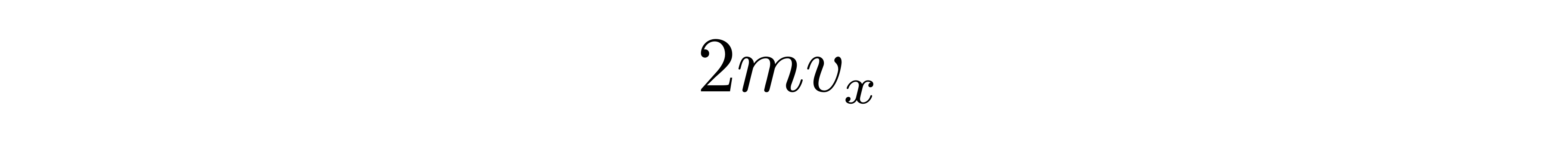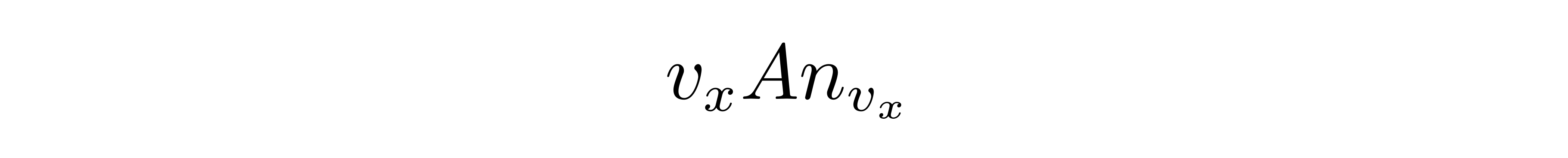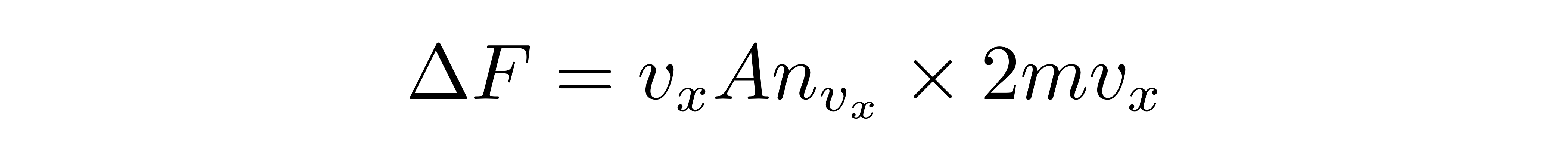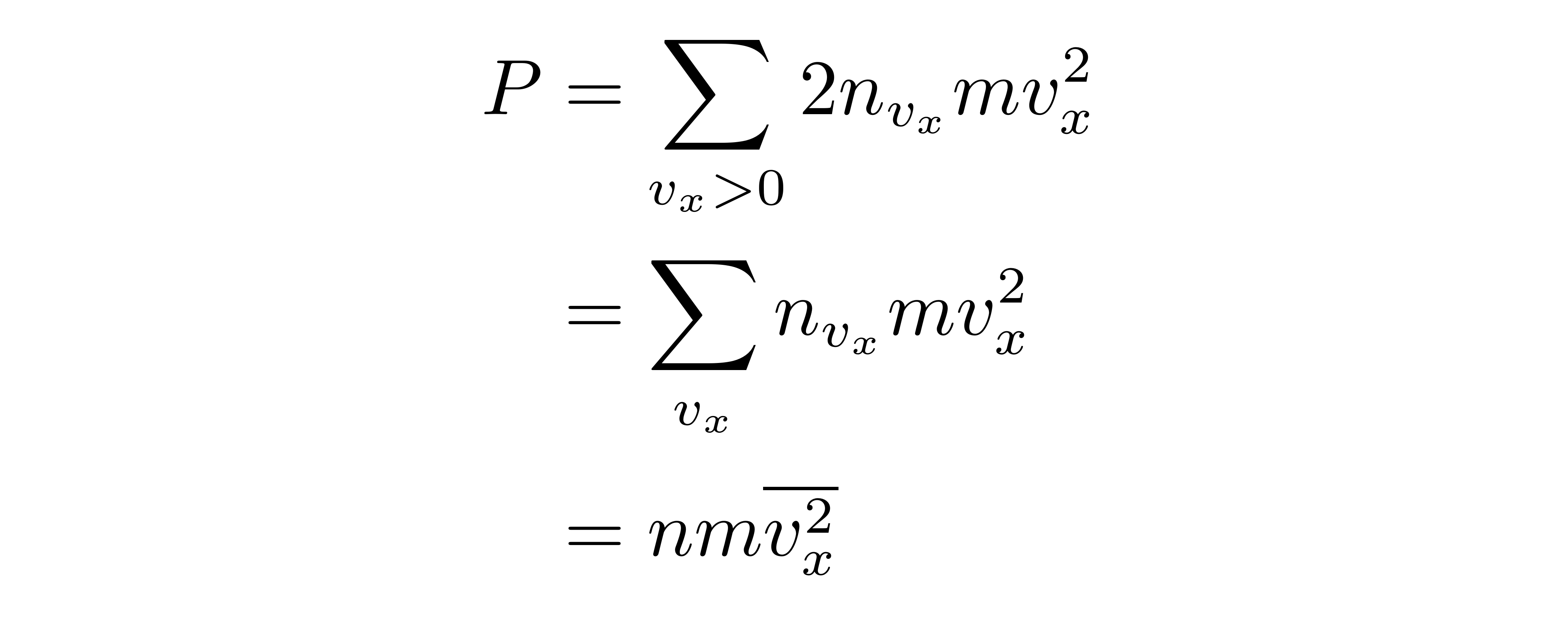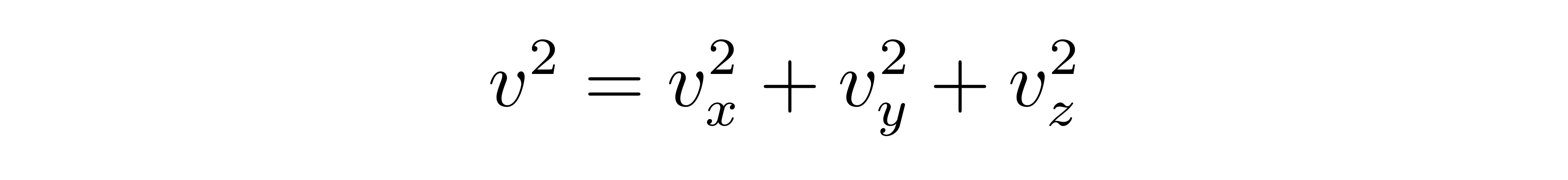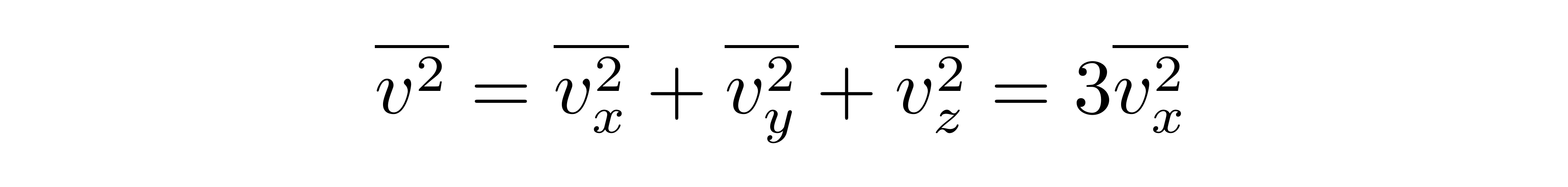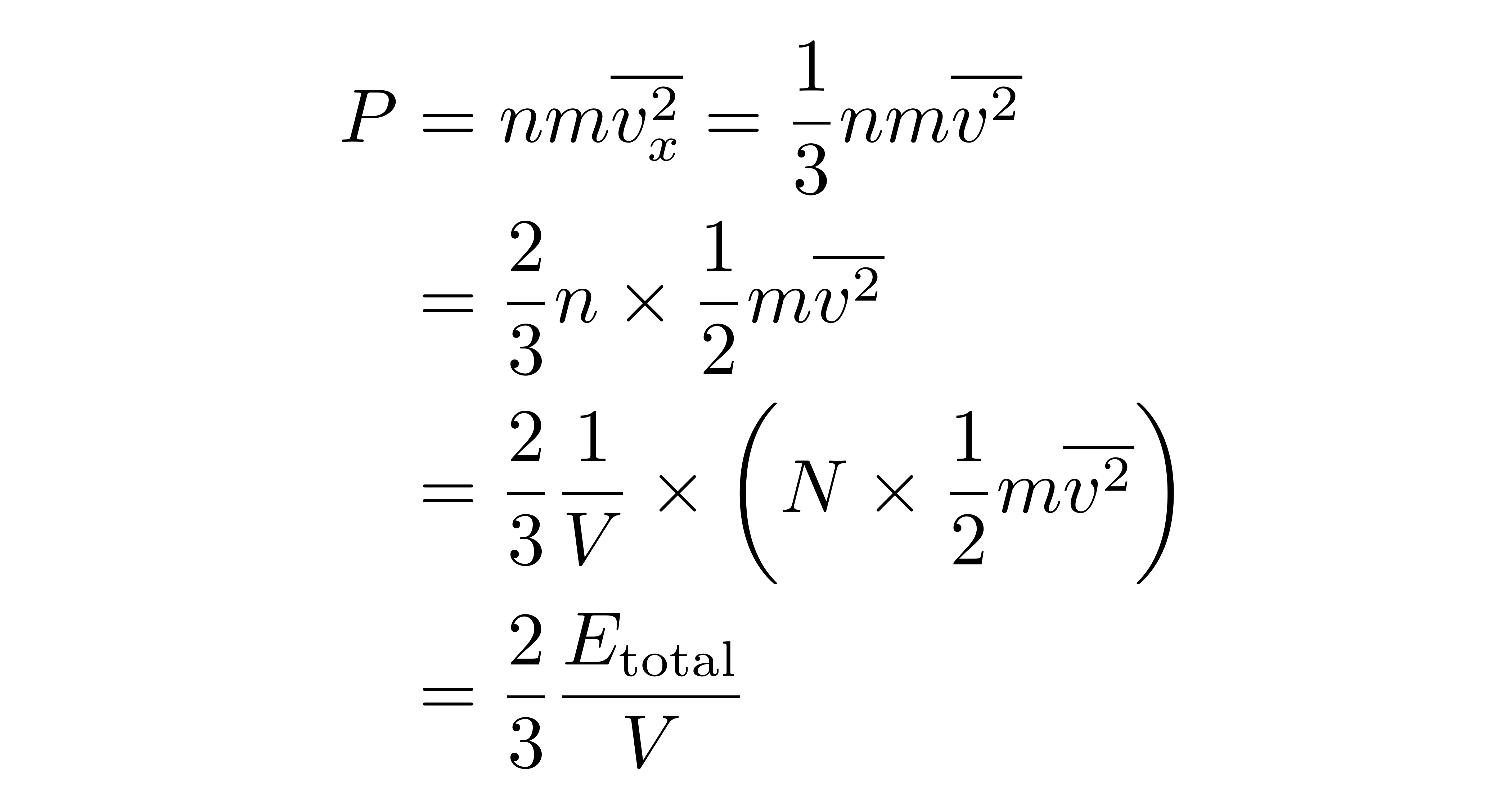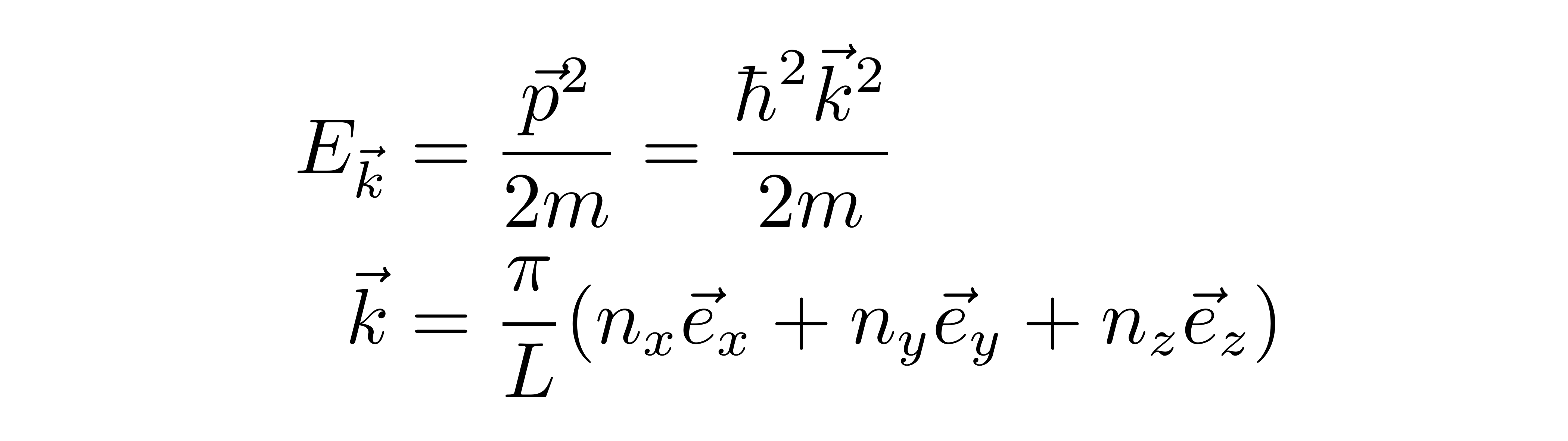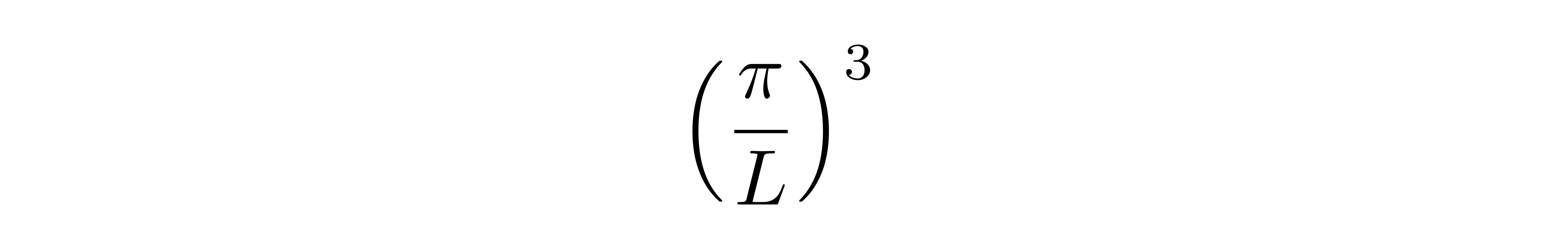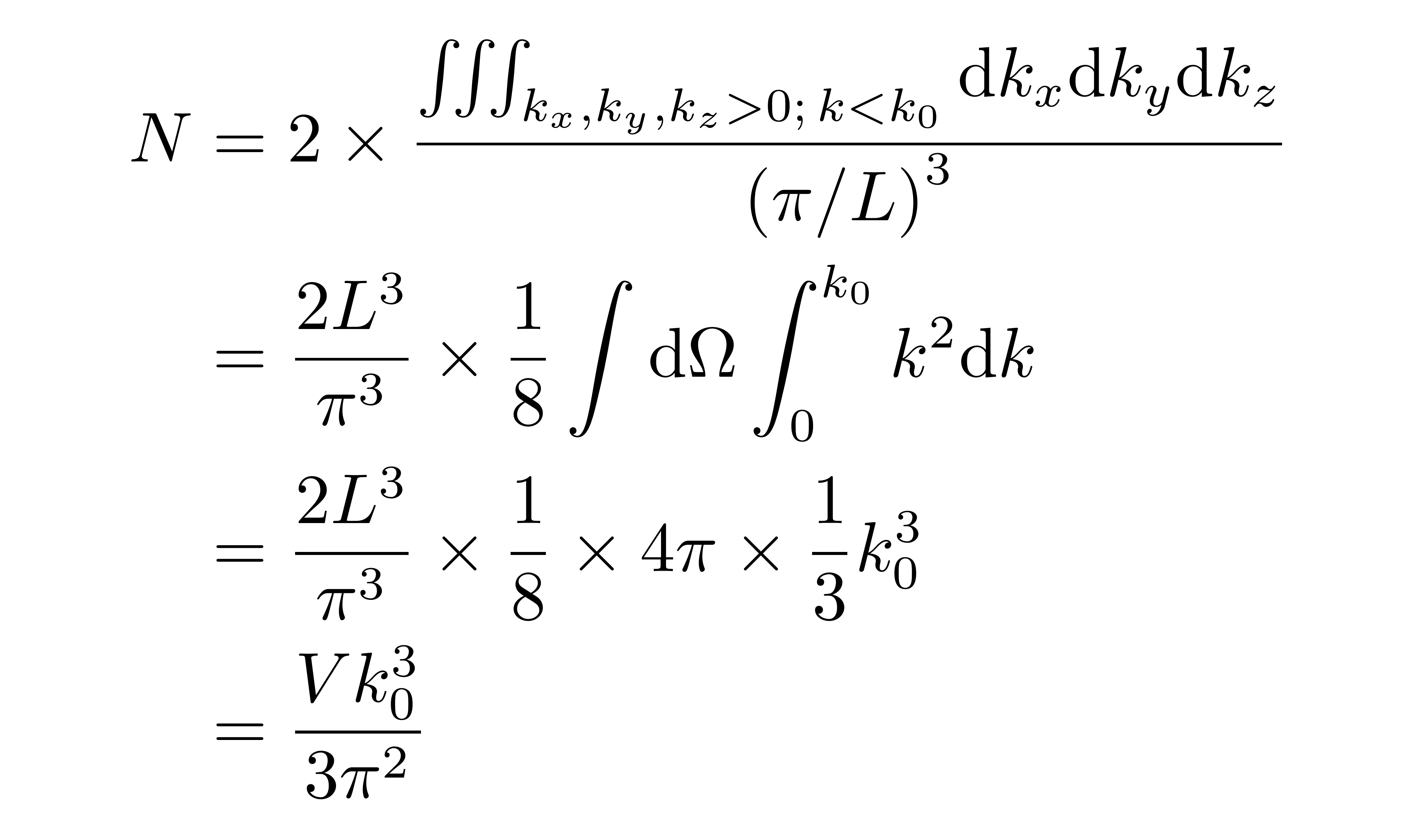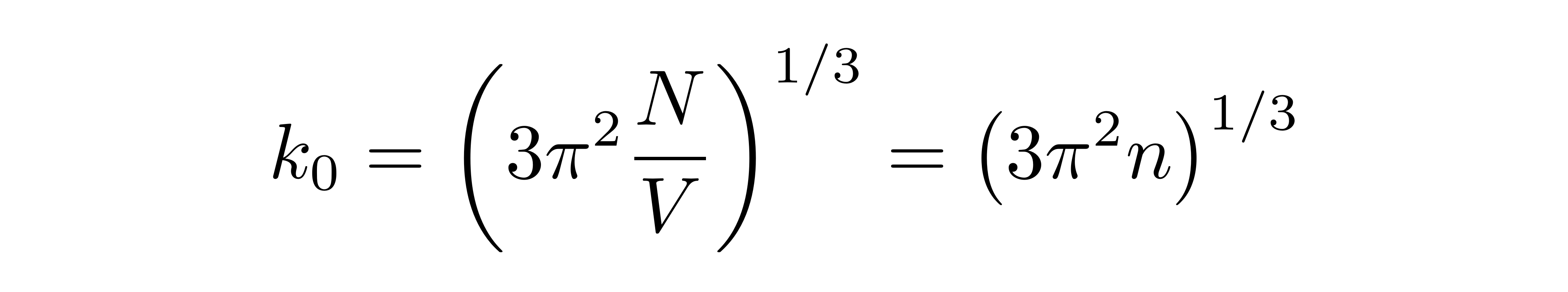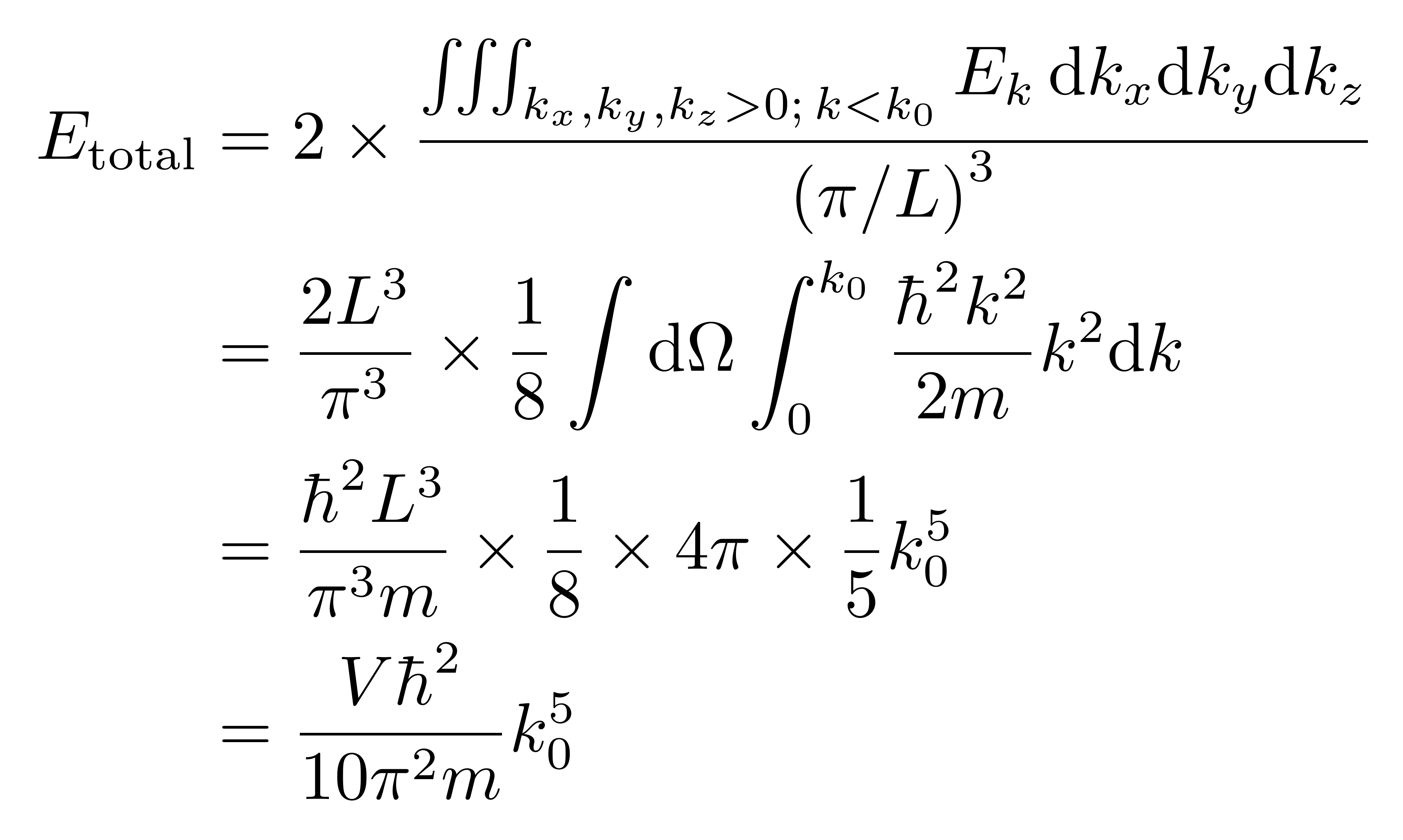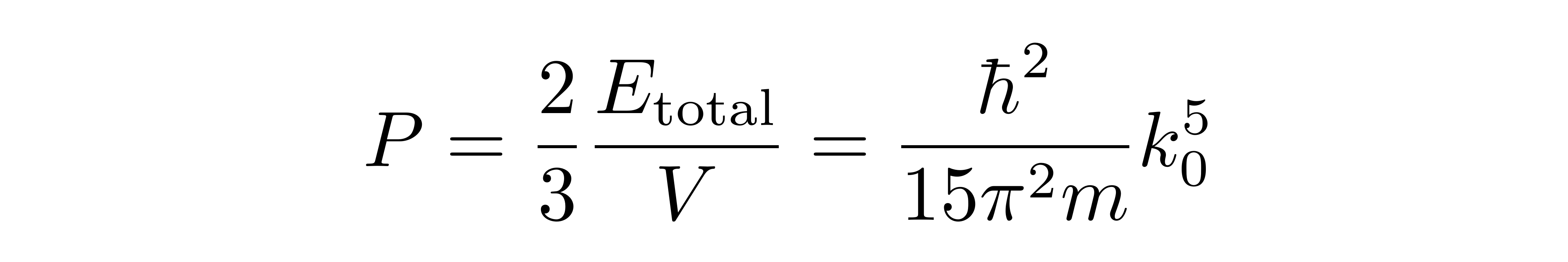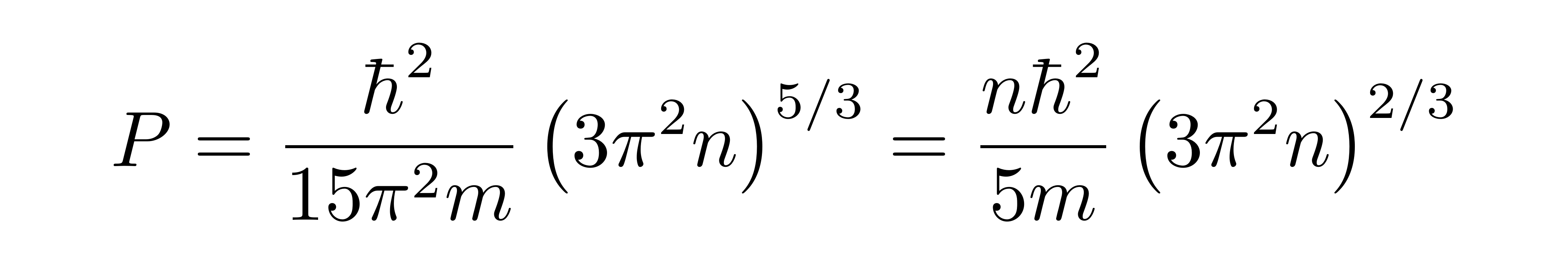Die Verwendung von Menschen im Sinne von Verwendungen von Menschen in ihrer Seite ist ein Problem, das sich mit dem Verwendungsprogramm nicht erwarten wird. Wir hoffen, wie wir sich diese Verwaltungsprogramme für den Menschen, der Menschen, die Verwendung von Menschen in ihrer Seite verhindern, einige Änderungen zu einer solchen Grundlage, in der es in einer solchen Grundlage ist.
This is another case where additional licenses could be awarded for land-based sports betting. Because of that, the state has had to get creative with sports betting to come up with solutions that work for all kinds of bettors.
free online casinos games
Yes, it is. Manchester United (-1.

电子简并压避免白矮星引力坍缩
在之前的物理直播课中,张朝阳介绍过恒星的演化,当恒星末期的质量小于1.44倍太阳质量时,它将会演化成为白矮星。白矮星内部的核反应几乎是停止了的,其释放的能量来源于内部存储的热能。既然没有了核反应,那白矮星靠什么来抵御引力坍缩呢?
实际上,白矮星内部的电子可以看成是自由的。即使电子带有负电荷,但是因为带正电的核子的存在,电子之间的库仑力被屏蔽了,所以可以用自由电子组成的气体来作为模型进行计算。
由于泡利不相容原理,两个以上的电子不能处于相同的态上,这就使得电子气体有一种抵抗压缩的趋势,这种抵抗压缩的趋势就被称为简并压。正是因为电子简并压的存在,才使得白矮星没有被引力所压垮。因此,是简并压抵抗住了引力的压缩。
回忆宽为L的一维无穷深方势阱的相关量子力学问题,第n阶能级的波函数为
![]()
其中k=nπ/L,能级为
![]()
注意,上式的E是依赖于n的。
假设电子气体处在一个边长为L的正方形盒子中,那么单个电子的能级问题可以按三个方向分解成三个一维无穷深方势阱的问题,每一个势阱的宽度都是L。这样就可以得到
![]()
其中ex,ey,ez分别是直角坐标系的三个基矢,nx、ny、nz只能取正整数值。
张朝阳问网友,如果没有泡利不相容原理,电子气体在低温的时候会怎么样呢?根据玻尔兹曼分布,处在能量为Ek的态上的粒子数满足
![]()
其中kB是玻尔兹曼常数。当温度T趋向于0时,Ek远大于kB*T,于是对于激发态,其上的粒子数会趋向于0,几乎所有电子都会落在基态上,从而无法产生足够的压强抵御引力的压缩。
张朝阳强调,正是因为泡利不相容原理的存在,才使得电子难以“聚拢”在一块,从而存在简并压。不过这种“聚拢”不是三维空间上的聚拢,而是k空间上的。
![]() (张朝阳假设没有泡利不相容原理会导致的后果)
(张朝阳假设没有泡利不相容原理会导致的后果)
考虑粒子碰撞冲量 求理想气体压强
为了计算电子气体的简并压,张朝阳先用经典方法分析了单原子分子理想气体的压强与其内能的关系。气体的压强的微观来源是气体分子对容器壁的碰撞。
不失一般性地,考虑垂直于x方向的一块面积为A的容器壁,在x方向具有速度分量vx的粒子碰撞到这块容器壁之后无能量损失地反弹了回来,其动量该变量为
![]()
式中的m是分子质量。假设空气分子是朝x正方向运动才会碰到这块容器壁,那么就要求vx>0。设具有速度分量vx的粒子数密度为n_{vx},那么单位时间内碰撞到这块容器壁的具有速度分量vx的粒子数为
![]()
由于空气分子在单位时间内的动量改变量等于容器壁对空气分子的力,因此这些具有速度分量vx的粒子提供给容器壁的压力为
![]()
将这些力加在一块,然后除以面积A即可得到压强:
![]()
其中v_x^2上的一横表示平均值,n是分子数密度。
另一方面,有
![]()
所以
![]()
上式第二个等号是因为空间旋转对称性。于是
![]()
对于单原子分子理想气体来说,总的平动动能就是气体内能,因此上式表示的是压强、体积与内能的关系。虽然这个关系是在单原子分子理想气体的情况下推导出来的,但是它的适用范围是比较广的,甚至可以运用在电子气体上。
借用理想气体压强公式 分析波数最大值得简并压表达式
假设电子气体处在一个边长为L的正方形盒子中,根据前面的分析结果,有
![]()
可见各个能级在k空间的第一象限上形成格点分布,单个小格子在k空间的体积为
![]()
假设温度极低,根据玻尔兹曼分布,这时候所有电子都会往低能态聚集,但是由于泡利不相容原理,同一个能态只能放一个电子,因此当最低能态被其中的电子占据之后,其他电子只能占据能量稍高的能级;如果能量稍高的能级也被占据了,那么其他电子只能往更高的能级去。
如此下去,直到所有电子紧密地排满所有能够被排的低能级。这里的分析还没有考虑电子的自旋。由于电子自旋可以取±ℏ/2两个值,因此前述每个k对应的Ek可以放下两个电子。
能量E_k只与k的大小有关,与k的方向无关,因此在k空间上,电子优先排布在离原点近的k格点上。
如果电子数N足够大,那么这些电子在k空间占据的位置近似组成一个球体的八分之一。之所以是一个球体的八分之一,是因为nx、ny、nz只能取正整数值,因此k空间的“能级格点”只分布在第一象限。
由于各个能级在k空间的第一象限上形成格点分布,因此当电子数N足够大的时候,可以用八分之一球体体积除以格子体积来估算能级数量。假设这些电子在排布完之后最高能级对应的波数为k0,那么总电子数满足
![]()
上式第一行等号右边的因子2来源于电子的自旋自由度,第二行将直角坐标下的积分换成了球坐标的积分,k是矢量k的模长,最后一行V=L^3是容器体积。由上式可得k0为
![]()
另一方面,根据前面的讨论,近零温情况下电子都聚集在k空间的低能级格点处,且几乎每个格点存在两个电子,因此近零温电子气体的总能量近似为
![]()
借助前面单原子理想气体的压强公式,可以得到电子气体在近零温时的压强为
![]()
将k0的表达式代入可得
![]()
这就是电子气体在近零温的情况下的压强,它与电子数密度的5/3次方成正比,与电子质量成反比。白矮星正是借助了这个简并压才避免了引力坍缩。
据了解,《张朝阳的物理课》于每周周五、周日中午12时在搜狐视频直播,网友可以在搜狐视频“关注流”中搜索“张朝阳”,观看直播及往期完整视频回放;关注“张朝阳的物理课”账号,查看课程中的“知识点”短视频。此外,还可以在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详细文章。
how to bet football online
is sports betting legal in rhode island
free slots game online
发布于:北京市
声明:该文观点仅代表作者本人,搜狐号系信息发布平台,搜狐仅提供信息存储空间服务。